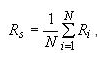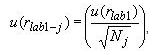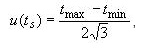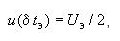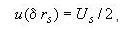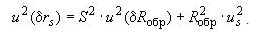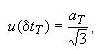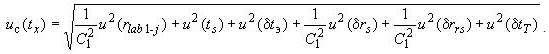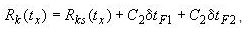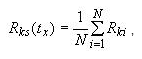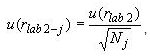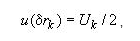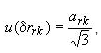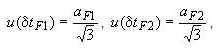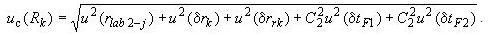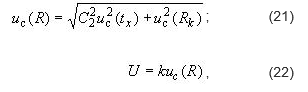11 Расчет расширенной неопределенности поверки термопреобразователей сопротивления в термостате или калибраторе
11.1 Суммарную стандартную и расширенную неопределенности поверки ТС рассчитывают для каждой температуры поверки. При расчете суммарной неопределенности поверки учитывают неопределенность измерений температуры эталонным (образцовым) термопреобразователем сопротивления и неопределенность измеренного значения сопротивления поверяемого ТС. Для расчета используют данные, полученные при проведении измерений (раздел 10), данные, полученные при предварительной экспериментальной оценке неопределенности, связанной со случайными эффектами при измерении в конкретной поверочной лаборатории (по 9.3), а также данные, приведенные в свидетельствах о поверке средств измерений: термостата, калибратора, реперной точки, эталонного термометра и измерительной установки.
11.2 При использовании сухоблочных термостатов (калибраторов) расчет неопределенности, приведенный в настоящей методике и основанный на данных свидетельства о поверке калибратора, относят только к поверке ТС диаметром, не превышающим 6 мм.
11.3 Значение температуры, определенное по показаниям эталонного термометра, рассчитывают по градуировочной характеристике эталонного термометра
tx=ƒ(Rs)
(4)
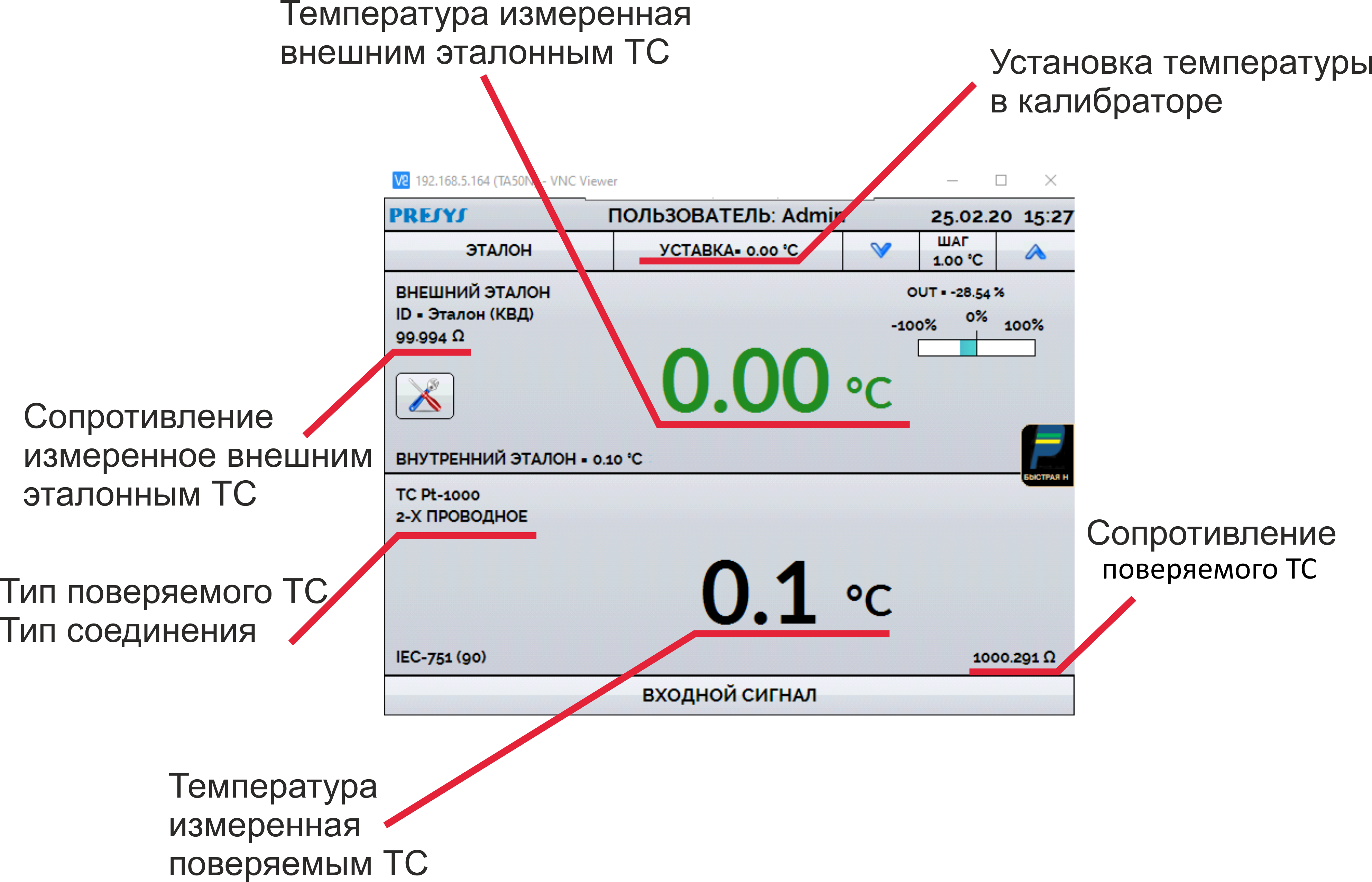
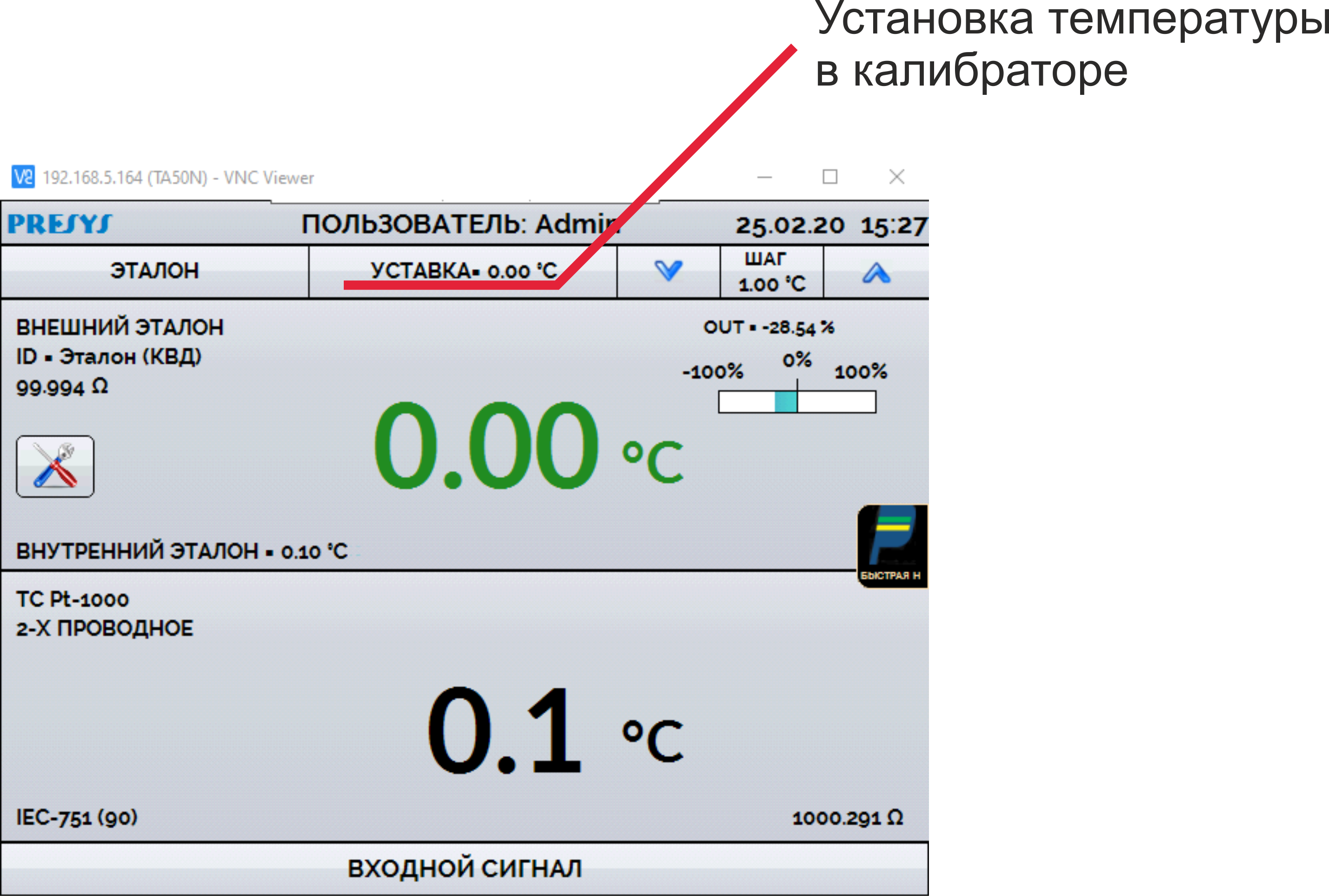
Желтым цветом будут подсвечены значения для расчёта неопределённости в точке 0
tx=0
где Rs- среднеарифметическое значение из результатов измерения температуры, определяемое по формуле
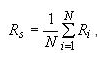
(5)
Rs=100
где N - число измерений сопротивления эталонного термометра, выполненных при градуировке;
N=5
Ri - значение, соответствующее i-му измерению сопротивления эталонного термометра.
11.4 Бюджет неопределенности для температуры, измеренной эталонным термометром, включает в себя следующие составляющие.
11.4.1 Стандартную неопределенность, обусловленную случайными эффектами при измерениях u(rlab1-j) , рассчитывают как СКО среднего значения результатов измерений, выполненных в одном измерительном цикле эталонным термометром по формуле
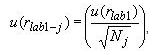
(6)
где u(rlab1) - СКО единичного измерения температуры эталонного термометра, определенное по 9.3;
Ri - число измерений в одном измерительном цикле.
11.4.2 Стандартную неопределенность, обусловленную
нестабильностью температуры в термостате за время всех
циклов измерений u(ts) , рассчитывают методом по типу В по формуле
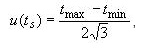
(7)
u(ts)=0,08660254
где tmax, tmin - соответственно максимальная и минимальная температура, измеренная эталонным термометром за время проведения всех измерительных циклов.
11.4.3 Стандартную неопределенность градуировки
эталонного термометра u(δtэ) рассчитывают по формуле
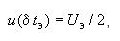
(8)
u(δtэ)=0,02
где Uэ - расширенная неопределенность градуировки
эталонного термометра при k=2, приведенная в свидетельстве о
его поверке (или доверительная погрешность при доверительной
вероятности 95%).
11.4.4 Стандартную неопределенность,
обусловленную неточностью электроизмерительной установки u(δrs) , при
использовании термопреобразователя сопротивления в качестве эталонного
термометра рассчитывают следующим образом:
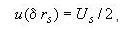
(9)
u(δrs)=0,016666667
где Us - расширенная неопределенность измерения при k=2, приведенная в свидетельстве о поверке установок для измерения сопротивления.
Примечания
1 Если в свидетельстве о поверке установки указан предел допускаемой
погрешности ±Δпр , то стандартную неопределенность
рассчитывают методом по типу В (нормальное распределение) по формуле u(δrs)=Δпр/3 .
Δпр=0,05
2 Если мост работает с внешней образцовой мерой
сопротивления и известны стандартная неопределенность измеряемого
отношения S=RTS/Rобр , а также стандартная
неопределенность градуировки меры u(δRобр) ,
то стандартную неопределенность измерения сопротивления ТС u(δrs) определяют
по формуле
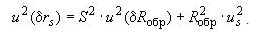
(10)
11.4.5 Стандартную неопределенность, вызванную ограниченной
разрешающей способностью отсчетных устройств электроизмерительной
установки u(δrrs) , оценивают по типу В по формуле

(11)
u(δrrs)=0,005773503
где ±ars - разрешающая способность установки для измерения сопротивления эталонного (образцового) термометра.
±ars=0,01
11.4.6 Стандартную неопределенность, обусловленную нестабильностью эталонного (образцового) термометра за межповерочный интервал , оценивают методом по типу В по формуле
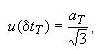
(12)
u(δtT)=0.0057735
где ±aT - интервал возможного изменения показаний эталонного термометра в тройной точке воды, определенный экспериментально при периодической поверке эталонного (образцового) термометра и приведенный в свидетельстве о его поверке.
±aT=0,01
11.5 Составляют бюджет неопределенности измерений температуры эталонным (образцовым) термометром (см. таблицу 2).
Таблица 2 - Бюджет неопределенности измерений температуры эталонным (образцовым) термометром
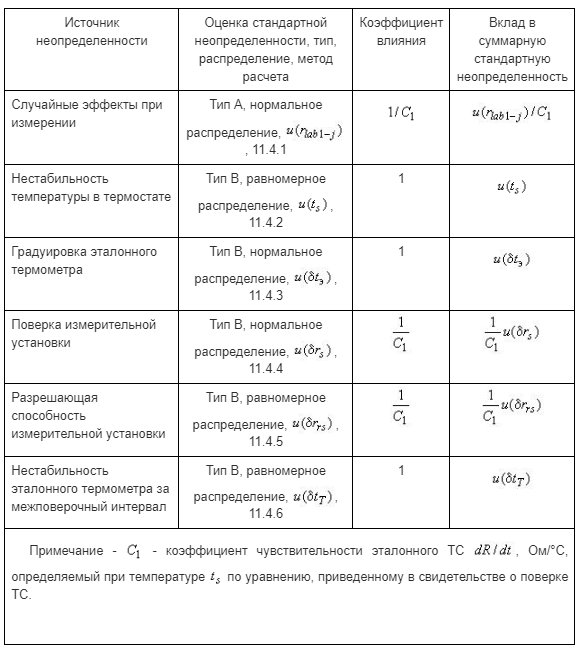
11.6 Суммарную стандартную неопределенность результата измерения температуры эталонным термометром рассчитывают по формуле
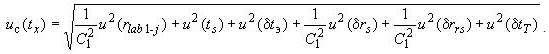
(13)
uc(tx)=0,09079892
Примечание - Расчет неопределенности измерения температуры при использовании эталонных термометров, для которых характерны другие функции преобразования, проводят аналогично вышеизложенному.
11.7 Значение сопротивления градуируемого ТС при температуре
tx-Rk(tx) рассчитывают по формуле
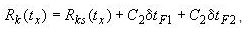
(14)
Rks(tx)=1000,1
Rk(tx)=1000,1
где C2 - коэффициент чувствительности ТС dR/dt , определяемый по уравнению НСХ ТС при температуре ;
δtF1 - поправка, равная изменению температуры по вертикальной оси рабочего объема термостата или калибратора между средней точкой ЧЭ поверяемого ТС и эталонного ТС;
δtF2 - поправка, равная изменению температуры по горизонтальной оси между ЧЭ поверяемого ТС и эталонного ТС (или между каналами блока сухоблочного калибратора).
Среднее значение сопротивления градуируемого ТС при температуре
tx-Rks(tx)
рассчитывают как среднеарифметическое значение результатов измерения сопротивления ТС при градуировке по 10.3.1 по формуле
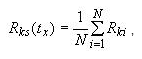
(15)
где N - число измерений сопротивления ТС;
Rki - результат i-го измерения сопротивления ТС.
Примечание - Поправки на вертикальный и горизонтальный
градиенты температуры вводят по результатам исследований термостата в
поверочной лаборатории. Если при поверке термостата или калибратора
градиент температуры был определен только в виде пределов отклонения
температуры от среднего значения
±aF1
, ±aF2 либо если неизвестна длина ЧЭ
поверяемых термопреобразователей, то поправки принимают равными нулю.
Градиент учитывают только введением неопределенности по 11.8.4.
11.8 Бюджет неопределенности измерений сопротивления ТС включает в себя следующие составляющие:
11.8.1 Стандартную неопределенность, обусловленную случайными
эффектами при измерениях, выполненных в одном измерительном цикле
поверяемым ТС, u(rlab2-j) оценивают по формуле
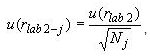
(16)
где u(rlab2) - СКО единичного измерения сопротивления ТС, определенное по 9.3;
Nj - число измерений сопротивления ТС в каждом цикле.
11.8.2 Стандартную неопределенность измерений при поверке
электроизмерительной установки u(δrk) рассчитывают следующим образом:
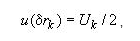
(17)
u(δrk)=0,01666667
где Uk - расширенная неопределенность измерения при k=2, приведенная в свидетельстве о поверке установки для измерения сопротивления ТС.
Примечание - Если в свидетельстве о поверке установки указан предел
допускаемой погрешности ±Δпр , то стандартную неопределенность рассчитывают
методом по типу В (нормальное распределение) по формуле u(δrk)=Δпр/3.
11.8.3 Стандартную неопределенность, обусловленную ограниченной
разрешающей способностью отсчетных устройств электроизмерительной
установки u(δrrk), рассчитывают по формуле
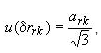
(18)
u(δrrk)=0,0057735
где ±ark - разрешающая способность установки для измерения сопротивления ТС.
11.8.4 Стандартные неопределенности, обусловленные вертикальным и
горизонтальным градиентами температуры в термостате или калибраторе
u(δtF1), u(δtF2) , рассчитывают по формулам
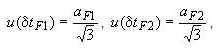
(19)
u(δtF1)=0,1471
u(δtF2)=0,1471
где ±aF1, ±aF2 - диапазон изменения
поправок к температуре, оцениваемый экспериментально при поверке
термостата или калибратора. Для использования значений ±aF1, ±aF2, в оценках
необходимы данные о том, как и с помощью каких по размерам термометров
они были получены.
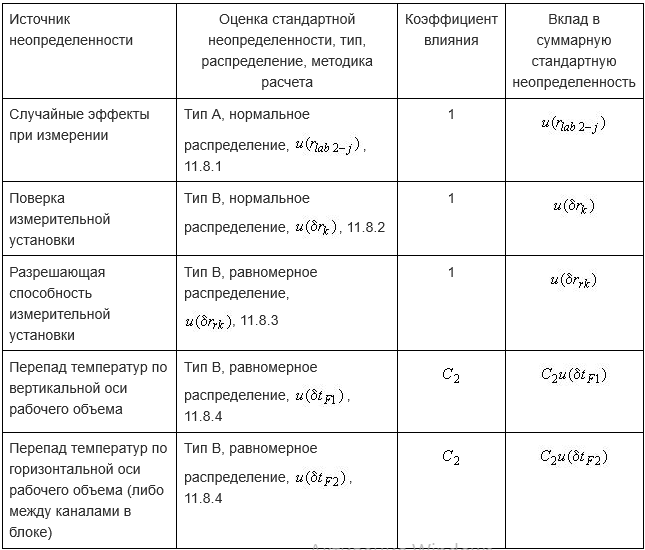
11.9 Бюджет неопределенности измерения сопротивления ТС представлен в таблице 3.
Таблица 3 - Бюджет неопределенности измерения сопротивления градуируемого термопреобразователя сопротивления
11.10 Суммарную стандартную неопределенность измерения сопротивления ТС
uc(Rk) оценивают по формуле
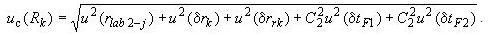
(20)
uc(Rk)=0,813319
11.11 Суммарную стандартную неопределенность uc(R) и расширенную
неопределенность U поверки ТС в каждой температурной точке
рассчитывают по формулам
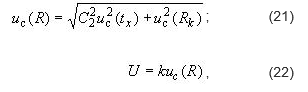
uc(R)=0,887382
U=1,774763
где k - коэффициент охвата.
11.12 Результат поверки
При k=2 сопротивление градуируемого термопреобразователя при
температуре находится в интервале Rk(tx)±U с вероятностью 95% в предположении
нормального закона распределения. Неопределенность поверки ТС в
единицах температуры рассчитывают делением U на коэффициент
чувствительности C2 .
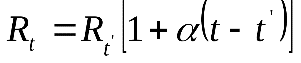 (1)
(1)
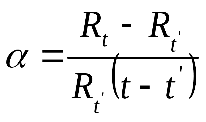 - температурный коэффициент сопротивления. (2)
- температурный коэффициент сопротивления. (2)
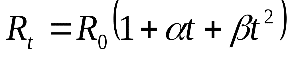 (3)
(3)